Se existem n1 resultados possíveis para um primeiro evento e n2 para um segundo, então existem n1. n2 resultados possíveis para a seqüência dos dois eventos.
Exemplo 1
Uma pessoa possui 3 camisas: uma branca (b), uma azul (a) e uma verde (v) e 2 calças: uma jeans (j) e uma preta (p). De quantas maneiras diferentes ela pode se vestir com uma calça e uma camisa?
Você pode escolher qualquer uma das 3 camisas, e para cada camisa escolhida pode optar por qualquer uma das duas calças.
Podemos resolver esse problema separando a tarefa de escolha das roupas em duas etapas seqüenciais: escolher primeiro a camisa e depois a calça.
Para melhor visualizar esse problema faremos uso da árvore de possibilidades:
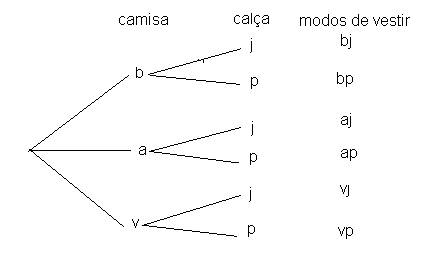 Fig 1 |
A árvore da fig 1 mostra que existem 3 X 2 = 6 possibilidades: {b,j}, {b,p},{a,j},{a,p},{v,j},{v,p}.
Nesse problema a seqüência dos eventos poderia ser trocada; a pessoa poderia escolher primeiro a calça e depois a camisa, resultando na seguinte árvore de possibilidades:
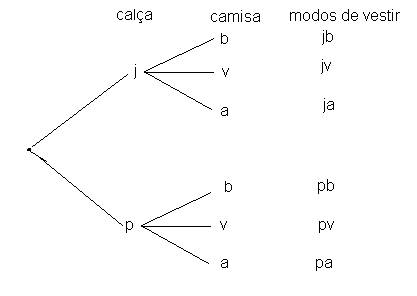 Fig 2 |
Nesse caso a árvore da fig 2 mostra que o número de possibilidades é o mesmo (2X3 = 6). Pensar em uma seqüência de eventos sucessivos nos ajuda a resolver o problema, mas a ordem da seqüência não faz parte do problema, pois o conjunto { j,b} é igual a {b,j}
Esse exemplo ilustra o fato de que o número total de resultados possíveis para uma seqüência de eventos pode ser obtido multiplicando-se o número de possibilidades do primeiro evento pelo número de possibilidades do segundo. Essa é a idéia do Princípio da Multiplicação.
O Princípio da Multiplicação pode ser estendido, por indução, a uma seqüência com qualquer número finito de eventos. O Princípio da Multiplicação é útil sempre que quisermos contar o número total de possibilidades para uma tarefa que pode ser divida em uma seqüência de etapas sucessivas.
Exemplo 2
A última parte do seu número de telefone contém quatro dígitos. Quantos desses números de quatro dígitos existem?
Podemos construir números de quatro dígitos através de uma seqüência de tarefas: escolher o primeiro dígito, depois o segundo, depois o terceiro e, finalmente o quarto. O primeiro dígito pode ser qualquer um dos dez dígitos, de 0 a 9, de modo que há dez possibilidades para a primeira tarefa. Da mesma forma, existem 10 escolhas diferentes possíveis para cada um dos segundo, terceiro e quarto dígitos. Usando o princípio da multiplicação, simplesmente multiplicamos o número de possibilidades para cada tarefa na seqüência. Portanto, existem 10.10.10.10= 10.000 números diferentes.
Exemplo 3
Com relação ao exemplo 2, quantos números de quatro dígitos existem se um mesmo dígito não puder ser repetido?
Novamente, temos uma seqüência de tarefas para selecionar os quatro dígitos, só que agora não podemos ter repetições. Temos 10 possibilidades para o primeiro dígito mas apenas 9 para o segundo, já que não podemos escolher um dígito igual ao primeiro, e assim por diante. Existem 10.9.8.7= 5.040 números diferentes.