Matemática Discreta Unidade D – Relações e Funções

Tipos de funções

Função injetora

Uma função f:AB é injetora se quaisquer dois elementos distintos de A, sempre possuem imagens distintas em B, isto é,

se x₁x₂ em A  f(x₁)f(x₂) em B

ou de forma equivalente,   f(x₁)=f(x₂) em B  x₁=x₂ em A

Nos exemplos a seguir, considere  o conjunto dos números reais.

 

Função sobrejetora

Uma função f: AB é sobrejetora, se todo elemento de B é imagem de pelo menos um elemento de A.

Desta forma, para todo y em B, existe x em A tal que y=f(x), isto é, Im(f)=B.

No diagrama a seguir, f: AB é sobrejetora, mas não injetora.

 

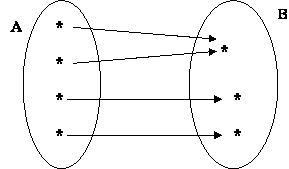
Diagrama de Função Sobrejetora

Exemplos:

a) A função f:  definida por f(x)=3x+2 é sobrejetora, pois todo número real é imagem de algum número real pela função f.

b) A função f:   definida por f(x)=x² é sobrejetora, pois todo elemento pertencente a é imagem de pelo menos um elemento de   pela função.                   

Observação:

Note que:

4 é imagem de -2 e 2  pois f(-2)=(-2)²=4 e f(2)=2²=4.

1 é imagem de –1 e 1 pois f(-1)=f(1)=1.

c) A função f:   definida por f(x)=x² não é sobrejetora, pois se considerarmos um número y<0, não encontraremos x tal que f(x)=y.

Função bijetora

Uma função f: AB é bijetora se f for, simultaneamente, injetora e sobrejetora. Quando isto ocorre, dizemos que há uma correspondência biunívoca entre A e B.

 

Seja a função f: AB f é injetora se todo elemento de B é imagem de um único elemento de A. f é sobrejetora se não sobra elemento em B que seja imagem de algum elemento em A, isto é, f(A)=B.

 

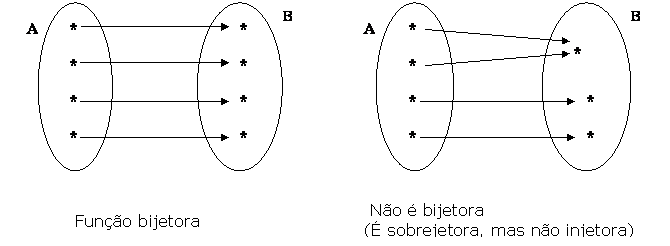
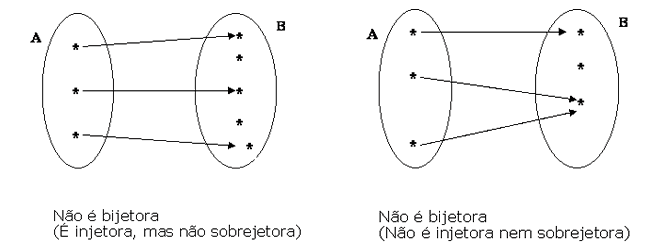
Exemplo

a) A função f:  dada por f(x)=2x é bijetora, pois é injetora e sobrejetora.

b) A função f:   definida por f(x)=x² não é bijetora, pois embora seja sobrejetora, ela não é injetora.

-33 mas f(3)=f(-3)=9.

Função composta

Dadas as funções f: AB e g: BC, a composta de f com g, denotada por gof, é a função definida por (gof)(x)=g(f(x)).

A composta gof pode ser lida como "g bola f".

Exemplo: Sejam as funções reais definidas por f(x)=4x+2 e g(x)=7x-4. As composições fog e gof são possíveis e neste caso serão definidas por:

(fog)(x) = f(g(x)) = f(7x-4) = 4(7x-4)+2 = 28x-14

(gof)(x) = g(f(x)) = g(4x+2) = 7(4x+2)-4 = 28x+10

Observação: Em geral, fog é diferente de gof.

Exemplo: Consideremos as funções reais definidas por f(x) = x²+1 e g(x) = 2x-4. Então:

(fog)(x) = f(g(x)) = f(2x-4) = (2x-4)²+1 = 4x²-16x+17

(gof)(x) = g(f(x)) = g(x²+1) = 2(x²+1)-4 = 2x²-2

Função inversa

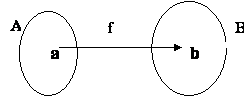
Dada uma função bijetora f: AB, denomina-se função inversa de f à função g: BA tal que se f(a)=b, então g(b)=a, quaisquer que sejam a em A e b em B.

Denotamos a função inversa de f por f ^-1.

 

Sejf: AB uma função bijetora e f -1 a inversa de f. Então:

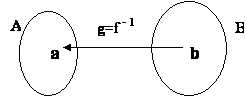 f ^-1(f(x)) =x   e  f(f ^-1(x))=x

Esta característica algébrica permite afirmar que, os gráficos de f e de sua inversa f ^-1, são simétricos em relação à função identidade (y=x).

Exemplo:

Sejam A={1,2,3,4,5}, B={2,4,6,8,10} e a função f:AB definida por f(x)=2x e g:BA definida por g(x)=x/2. Observemos nos gráficos as situações das setas indicativas das ações das funções.

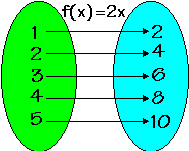
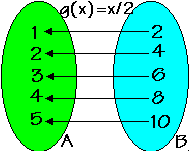
Observação: g(x)=f ^-1(x)

Obtenção da inversa:

Seja f: , f(x)=x+3. Tomando y no lugar de f(x), temos y=x+3. Trocando x por y e y por x, temos,  x=y+3

Isolando y obtemos y=x-3. Assim,
                         f ^-1(x) = x-3 é a função inversa de f(x)=x+3.

Observe que se f ^-1(x) = g(x), temos

g(f(x)) = g(x+3) = (x+3)- 3 = x  e

f(g(x)) = f(x-3) = (x-3)+3 = x

Observando o gráfico a seguir, identificamos a simetria em relação à reta y=x (função identidade).

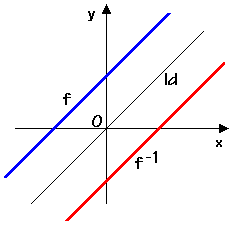f(x)=x+3 f -1(x)=x-3 Id: y=x