Matemática Discreta Unidade D – Relações e Funções

Função

Estudaremos agora um tipo particular de relação entre conjuntos. Esse tipo de relação, por possuir uma propriedade especial, será chamada de função.

Consideremos a relação f de A em B, descrita pelo diagrama abaixo.

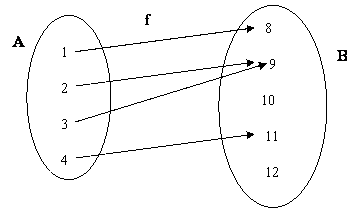
Note que todo elemento de A está associado, através de f, a um único elemento de B. Essa propriedade caracteriza uma função e por isso dizemos que f é uma função de A em B.

Definição    

Sejam A e B conjuntos diferentes do vazio. Uma relação f de A em B é função se, e somente se, todo elemento de A estiver associado, através de f, a um único elemento de B.

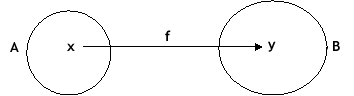
Usaremos a notação f: AB para indicar que f é função de A em B.

Seja f uma função de A em B, então: A é o Domínio de f, representado por D(f). B é o Contradomínio, cuja notação é CD(f). Todos os elementos de B, que estão associados pela função f, pertencem ao conjunto denominado Imagem, representado por Im(f). Se y estiver associado a x, através de f, conforme o diagrama abaixo, então dizemos que y é imagem de x, e indicaremos este fato por y=f(x).

Exemplos
a)
 

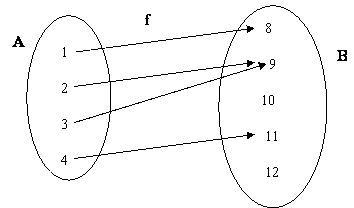
f é função de A em B, pois todo elemento de A está associado, através de f, a um único elemento de B.

f(1)=8 (8 é imagem de 1 através de f)

f(2)=9 (9 é imagem de 2 através de f)

f(3)=9 (9 é imagem de 3 através de f)

f(4)=11 (11 é imagem de 4 através de f)

D(f)={1,2,3,4}, Im(f)={8,9,11}, CD(f)=B

b)

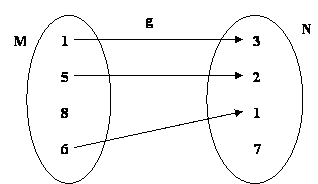
g não é função de M em N, pois existe elemento em M que não está associado, através de g, a algum elemento de N.

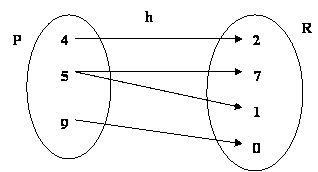
h não é função de P em R, pois o elemento 5 está associado, através de h, a mais de um elemento de R.