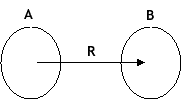
Relação
Dados dois conjuntos A e B, quando dizemos que um elemento a de A está relacionado a outro elemento b de B, por uma relação R, estamos fazendo uma afirmação sobre o par ordenado (a,b) no produto cartesiano AxB. Portanto, uma definição matemática de uma relação pode ser dada em termos de pares ordenados no produto cartesiano de conjuntos.
Definição
Sejam A e B conjuntos. Uma Relação R de A em B é um subconjunto de um produto cartesiano AxB, ou seja: R
AxB
É costume denotar (a,b)
R por aRb. O símbolo aRb é lido “a está relacionado com b”.
Exemplo
Em uma comunidade X, temos que Alberto (a) é marido de Beatriz (b) e Carlos (c) é marido de Daniela (d). No entanto, Eugênio (e), Francisco (f), Helena (h) e Janaína (j) são solteiros.
Considere a relação M (de ser marido de ...). O símbolo aMb ou (a,b)M pode ser lido “a é marido de b”.
Pela definição, a relação M é o seguinte conjunto: {(a,b), (c,d)}, pois a é marido de b, c é marido de d.
Comentários
Se considerarmos o conjunto dos homens A={a, c, e, f} e das mulheres B={b, d, h, j}, temos o seguinte conjunto formado por pares,
AxB={(a,b),(a,d),(a,h),(a,j),(c,b),(c,d),(c,h),(c,j),(e,b),(e,d),(e,h),(e,j), (f,b),(f,d),(f,h),(f,j)}
Note que a relação M é subconjunto de AxB.
| ||||
| ||||
|
Exemplo
Sejam A={a}, B={a,b} e C={0,1,2}, então são relações:
a) Como AxBAxB, segundo a definição,
AxB = {(a,a),(a,b)} é uma relação com origem em A e destino B.
b) Considerando o conjunto de partida A e o conjunto de chegada B, a relação de igualdade é {(a,a)}.
c) {(0,a), (1,b)} é uma relação de C em B.
Observação: Uma relação RAxB também é denotada como segue:
R:A
B
Exemplo
Sejam B = {a,b} e C = {0,1,2}. Então:
a) BxC={(a,0),(a,1),(a,2),(b,0),(b,1),(b,2)}
b) Para a relação 
: C C, tem-se que 01, 02 e 12.
c) Para a relação = : B B, tem-se que a=a e b=b.
Representação de relação, utilizando diagrama de Venn
Uma relação R: AB pode ser representada usando Diagrama de Venn. Nesse caso, dois elementos relacionados são ligados por uma seta, com origem no elemento do conjunto de partida e destino no elemento do conjunto de chegada.
Exemplos
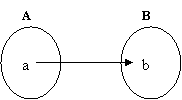
Sejam A = {a}, B = {a,b} e C = {0,1,2}.
a) O par (a,b) da relação R: AB pode ser representado por,
b) Para a relação : CC, temos
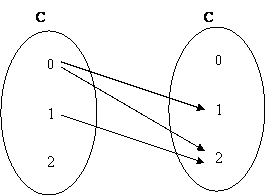
Esta relação pode ser escrita da seguinte forma:
(C,) = {(0,1),(0,2),(1,2)}
Quando relacionamos entidades de um mesmo conjunto, esta relação recebe o nome de endorrelação.
Endorrelação
Definição: Suponha A um conjunto. Então uma relação R:AA (origem e destino no mesmo conjunto) é dita uma Endorrelação ou Auto-relação. Nesse caso, afirma-se que R é uma relação em A.
Uma endorrelação R: AA é frequentemente denotada por: (A,R)
Domínio de Definição, conjunto imagem
Definição: Seja R:AB uma relação. Então:
a) Se (a,b)R, então se afirma que b é imagem de a.
b) O conjunto de todos os elementos de A para os quais R está definida é denominada Domínio.
c) O conjunto de todos os elementos de B, imagem de R, é denominado Conjunto Imagem.
Notação:
Domínio da Relação R: D(R)
Conjunto Imagem: Im(R)
Exemplos:
Sejam B = {a,b} e C = {0,1,2}.
a) Para a endorrelação (C,), dado que a relação é definida pelo conjunto
{(0,1), (0,2), (1,2)}.
D(R)={0,1}, Im(R)={1,2}.
b) Para a endorrelação (B,=), o conjunto {a,b} é o domínio de definição e o conjunto imagem.
D(R)=Im(R)={a,b}.
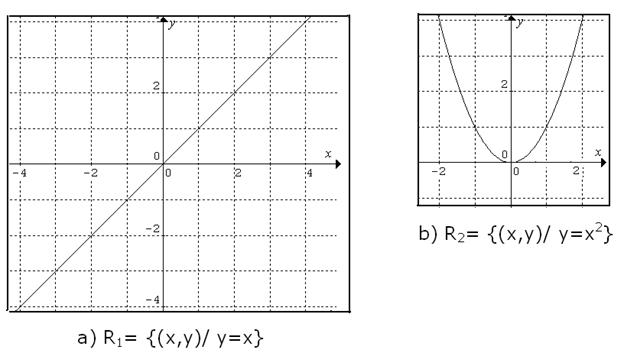
Representação de relação no plano cartesiano
Exemplos: Considere as seguintes relações no conjunto dos números reais.
Relação como matriz
A representação de uma relação R:AB na forma de uma matriz é interessante para implementação em um sistema computacional.
Seja A={a1, a2, a3, ..., an} e B={b1, b2, b3, ..., bm}
| R | b1 |
b2 |
b3 |
... |
bm |
a1 |
V |
F |
F |
... |
V |
a2 |
V |
F |
V |
... |
F |
a3 |
F |
V |
F |
... |
F |
: |
: |
: |
: |
: |
|
an |
V |
F |
V |
... |
V |
Se (ai,bj)R, então a posição da matriz determinada pela linha i e coluna j contém o valor lógico verdadeiro (V); caso contrário, contém o valor lógico falso (F). Por simplicidade visual, nas matrizes serão utilizados os dígitos 0 e 1 no lugar de F e V, respectivamente.
Exemplo
Seja B={a,b}. Represente a seguinte endorrelação completando a matriz.
A relação (B,=) é definida por {(a,a), (b,b)}.
Resposta
= |
a |
b |
a |
1 |
0 |
b |
0 |
1 |
Lembre-se que 1 representa o valor lógico V e 0 representa F.
Atividade D1
Sejam B={a,b} e C={0,1,2}. Represente as endorrelações, completando as matrizes correspondentes.
a) (C,<) = {(0,1),(0,2),(1,2)}.
| < | 0 |
1 |
2 |
0 |
|
|
|
1 |
|
|
|
2 |
|
|
|
b) (C,>) = {(1,0),(2,0),(2,1)}.
| > | 0 |
1 |
2 |
0 |
|
|
|
1 |
|
|
|
2 |
|
|
|
c) R:CC tal que R={(0,2),(2,0),(2,2)}
| R | 0 |
1 |
2 |
0 |
|
|
|
1 |
|
|
|
2 |
|
|
|