Expressões

O termo expressão, levando-se em consideração o computador, está ligado diretamente ao conceito de expressão ou fórmula matemática, em que o conjunto de variáveis e constantes numéricas relacionam-se através de operadores aritméticos, determinando uma fórmula, sendo que esta ao ser avaliada, vai determinar um valor, que é o resultado da expressão matemática.

1 Expressões Aritméticas

Expressões aritméticas são aquelas cujo resultado da avaliação é do tipo numérico, seja ele inteiro ou real. Somente o uso de operadores aritméticos e variáveis numéricas, são permitidos em expressões deste tipo.

Os operadores aritméticos estão relacionados na tabela 1:

Operador	Tipo	Operação	Prioridade
+	Unário	Manutenção do sinal	1
-	Unário	Inversão do sinal	1
** ou^	Binário	Exponenciação	2
*	Binário	Multiplicação	3
/	Binário	Divisão	3
+	Binário	Adição	4
-	Binário	Subtração	4

Tabela 1 - Operadores aritiméticos

O tipo de operador binário indica que são necessários dois números para realizar a expressão, e o tipo unário indica que apenas um é necessário para realizar a expressão.

A prioridade entre operadores define a ordem em que os mesmos devem ser avaliados dentro de uma mesma expressão.

A prioridade 1 para um operador é a que deve ser realizada antes de todas as outras operações.

A prioridade 2 para um operador é a que deve ser realizada antes dos operadores de prioridade 3 e 4 mas depois do operador de prioridade 1.

A prioridade 3 para um operador é a que deve ser realizada antes dos operadores de prioridade 4 mas depois do operador de prioridade 1 e 2.

As operações com operadores de prioridade 4, são as realizadas após todas as outras operações que possuem operadores de prioridade 1, 2 e 3.

O caracter ( * ) é adotado na maioria das linguagens de programação para representar a operação de multiplicação, ao invés do caracter ( x ), pois é possível que este mesmo caracter seja usado com um nome de variável.

As variáveis usadas em expressões aritméticas podem ser somente do tipo inteiro ou real. Se todas as variáveis que aparecem numa expressão são do tipo inteiro, então o resultado da expressão também é do tipo inteiro. Se, pelo menos, uma variável é do tipo real, então o resultado da expressão será do tipo real.

2 Expressões Lógicas e seus Operadores Lógicos

Expressões lógicas são aquelas cujo resultado da avaliação é um valor lógico (V ou  F).

Pode ser que você precise, em qualquer momento, trabalhar com o relacionamento de duas ou mais condições ao mesmo tempo na mesma instrução, realizando testes múltiplos. Para esses casos, é necessário trabalhar com a utilização de operadores lógicos, também conhecidos como operadores booleanos.

Os operadores lógicos e suas prioridades são mostrados na tabela 2.

Para exemplificar o uso de operadores lógicos, as tabelas 3 e 4 apresentam as variáveis lógicas A e B. Uma vez que cada variável lógica possui somente dois valores possíveis, então há exatamente 4 combinações para estes valores, razão pela qual a tabela tem 4 linhas. As colunas contêm os resultados das operações lógicas sobre as combinações possíveis dos valores das variáveis A e B.

	Lembrando: ● O operador lógico NÃO, sempre inverte o valor de seu operando. ● Para que a expressão lógica com o operador OU tenha resultado verdadeiro, basta que um de seus operandos seja verdadeiro. ● O operador do tipo E é utilizado quando dois ou mais relacionamentos lógicos de uma determinada condição necessitem ser verdadeiros.

Para melhor visualizar, pode-se imaginar que as variáveis lógicas A e B são como dois interruptores ligados em paralelos num circuito de acionamento de uma lâmpada (Figura 1).

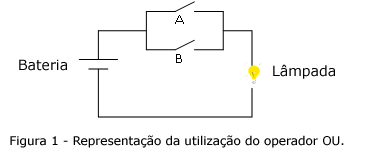
No exemplo acima, um interruptor fechado (permite a passagem de corrente elétrica) representa uma variável lógica cujo valor é verdadeiro (V), e um interruptor aberto representa uma variável lógica  com valor falso (F).

No circuito da Figura 1 (circuito elétrico com interruptores em paralelo), para que a lâmpada acenda, basta que qualquer um dos interruptores esteja fechado. Da mesma forma, para que uma expressão lógica que use o operador OU tenha resultado verdadeiro, basta que apenas um dos operandos possua valor lógico V. No entanto, para que a operação lógica OU tenha resultado F (lâmpada apagada) é preciso que os dois operandos possuam valor F (isto é, os dois interruptores abertos).

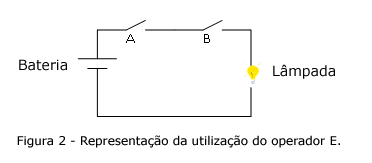
Já, para que a operação lógica E tenha resultado verdadeiro, é preciso que seus dois operandos tenham valor lógico verdadeiro. Em termos de um circuito elétrico, uma operação lógica E pode ser representada por dois interruptores ligados em série, como mostra a Figura 2.

No circuito, representado na Figura 2, a lâmpada somente estará acesa quando os dois interruptores (A e B) estiverem fechados. No entanto, se apenas um dos interruptores estiver aberto a lâmpada não acenderá. Da mesma maneira, a operação lógica E só resultará verdadeiro quando (A e B) forem iguais a V, e para que a operação lógica resulte em falso, basta que um dos seus operadores seja falso (F).

2.1 Operadores Relacionais

Os operadores relacionais são usados somente quando se deseja efetuar comparações. Comparações só podem ser feitas entre objetos da mesma natureza, isto é, variáveis do mesmo tipo de dado. O resultado de uma comparação é sempre um valor lógico.

Veja a tabela 5.

O uso de operadores relacionais possibilita o aparecimento em expressões lógicas de variáveis de outros tipos de dados que não o lógico.

Exemplo: Sejam A e B variáveis lógicas, X e Y variáveis reais, e R, S e W variáveis literais, com os seguintes valores:

A= V

B= F

X=0.25

Y=2.5,

R=”ANA”

S=”MÁRIO”

W=”ROSANA”

A tabela 6 contém algumas expressões lógicas contendo essas variáveis:

3  Expressões literais

Expressões literais são aquelas cujo resultado da avaliação é um valor literal.

Como exemplo, vamos concatenar (significa somar os caracteres) os literais “aspira” e “dor”, cujo resultado é: “aspirador”.

x = "aspira'
y = "dor"
z = x + y

Então a variável z conterá "aspirador".

4 Avaliação de Expressões

Expressões que apresentam apenas um único operador podem ser avaliadas diretamente. No entanto, à medida que elas vão ficando mais complexas com o aparecimento de mais de um operando na mesma expressão, é preciso avaliar esta expressão passo a passo, tomando um operador por vez.

A seqüência desses passos é determinada de acordo com o formato geral da expressão, considerando-se a prioridade de avaliação de seus operadores e a existência ou não de parênteses na referida seqüência.

As regras a seguir são essenciais para a correta avaliação de expressões:

1ª Deve-se observar a prioridade dos operadores, desta forma,  operadores de maior prioridade devem ser avaliados primeiro. Se houver empate em relação à precedência, então, a avaliação se faz, considerando-se a expressão da esquerda para a direita.

2ª Os parênteses usados em expressões “tomam” a prioridade dos demais operadores, forçando a avaliação da subexpressão em seu interior.

3ª Entre os quatro grupos de operadores existentes: aritmético, lógico, literal e relacional, há uma certa prioridade de avaliação, desta forma, os aritméticos e literais devem ser avaliados primeiro; a seguir, são avaliadas as subexpressões com operadores relacionais e, por último, os operadores lógicos são avaliados.

	Exemplo: Vamos supor que as variáveis X, Y e Z são variáveis reais, e A e B são variáveis lógicas, com os seguintes valores. X= 2.0, Y= 3.0, Z= 0.5, A= V e B= F Considere as seguintes expressões e o resultado de sua avaliação: 1) X * Y - Z = 5.5   6) X ** Y -1 = 7.0 2) X * (Y-Z) = 5.0   7) (X ** Y) -1 = 7.0 3) X + Y * Z = 3.5   8) X ** (Y -1) = 4.0 4) X + (Y * Z) = 3.5   9) B .E. A .OU. X<>Y/2 = .V. 5) (X + Y) * Z = 2.5   10) B .E. (A .OU. X<>Y/2) = .F.

Do exemplo acima, pode-se observar que:

• a aplicação da segunda regra faz com que a expressão 2 tenha um resultado diferente da expressão 1. O mesmo ocorre com as expressões 3 e 5, 6 e 8, 9 e 10.
• o agrupamento de subexpressões usando parênteses, contendo operadores de prioridade maior que a dos operadores que permaneceram fora dos parênteses, não altera a ordem de avaliação de expressões e,  não modifica seus resultados, como ocorreu em 3 e 4, 6 e 7.
• a aplicação da terceira regra define a única seqüência correta para se avaliar as expressões 9 e 10. De fato, esta regra define que a subexpressão Y/2 deve ser avaliada antes de se comparar seu resultado com X (em X<>Y/2). Se a comparação X<>Y fosse feita, seu resultado seria um valor lógico, que depois seria dividido por 2, o que é impossível.

5 Síntese

Uma expressão é uma combinação de variáveis, constantes e operadores, que resulta num valor,quando avaliada.

Operadores são elementos funcionais que atuam sobre operandos. Segundo o número de operandos sobre os quais atua, um operador pode ser classificado em unário ou binário. Segundo os tipos de dados de seus operandos e do valor resultante de sua avaliação, os operadores podem ser classificados em aritméticos, lógicos ou literais.

Um outro tipo de operador é o relacional, que é usado na comparação de operandos de um mesmo tipo de dado e cujo resultado da avaliação é sempre um valor lógico.

As expressões são classificadas de acordo com o valor resultante de sua avaliação em:

• aritméticas: que resultam num valor numérico, real ou inteiro;
• lógicas: que resultam num valor lógico;
• literais: que resultam num valor literal.

Há três regras básicas que determinam a seqüência correta de avaliação passo a passo de expressões:

1. Operadores de maior prioridade devem ser avaliados primeiro. Se houver empate, a avaliação é feita da esquerda para a direita.
2. O uso de parênteses em sub-expressões força a sua avaliação com maior prioridade.
3. Os diversos tipos de operadores devem ser avaliados na seguinte seqüência, dentro de uma grande expressão: primeiro os aritméticos e literais, em segundo os relacionais e, por último, os lógicos.