Os circuitos que compõem um computador são bastante complexos. Apenas uma parte dessa complexidade pode ser entendida a partir das leis de kirchhoff.

Num circuito com vários ramos, podem-se aplicar as Leis de Kirchhoff:

Lei dos nós

A soma das intensidades das correntes que chegam a um nodo é igual à soma das intensidades das correntes que partem desse nodo.

Lei das malhas

Numa malha, a soma algébrica das forças eletromotrizes é igual à soma algébrica das diferenças de potencial, ao longo dessa malha.

Um circuito elétrico pode ser composto por várias malhas, constituídas por elementos que geram ou absorvem energia elétrica. Devido à complexidade dos circuitos, é, muitas vezes, necessário utilizar as leis de Kirchhoff no cálculo das tensões e correntes nos elementos dos circuitos.

Um circuito é composto por malhas, nós e ramos. Define-se malha como sendo um circuito fechado, constituído por elementos elétricos. Denomina-se nó a um ponto de interligação de três ou mais componentes, e ramo ao trecho compreendido entre dois nós consecutivos.

A figura 1 mostra um circuito elétrico em que se exemplificarão os conceitos definidos anteriormente:

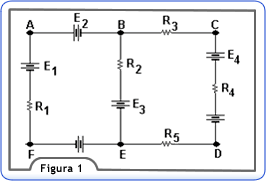
       Note-se que o circuito é composto por três malhas: ABEF, BCDE e ABCDEF; sendo esta última denominada malha externa. Entre os nós B e E encontram-se 3 ramos distintos (constituídos por geradores e resistências): o ramo à esquerda composto por E6, R1, E1 e E2, o ramo central composto por E3 e R2 e o ramo à direita composto por R5, E5, R4, E4 e R3. E6 E5.

Após estas considerações, podem-se enunciar as leis de Kirchhoff:

1ª Lei: Num nó, a soma algébrica das correntes é nula (i.e. a soma das correntes que entram no nó é igual à soma das correntes que saem).

Exemplo:

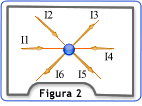
No nó A, consideram-se as correntes que chegam, como positivas e as que saem,
como negativas. Assim:

I1 + I2 – I3 + I4 – I5 – I6 =0

ou

I1 + I2 + I4 = I3 + I5 + I6

2ª Lei: Numa malha, a soma algébrica das tensões é nula.

Exemplo:

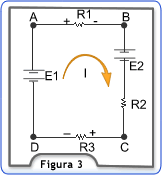
Circulando no sentido convencionado da corrente para a malha ABCD, pode-se escrever:

-VR1 + E2- VR2- VR3+ E1 = 0

Em que o sinal positivo representa um aumento de potencial e o sinal negativo uma perda de potencial.