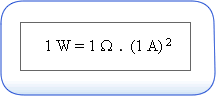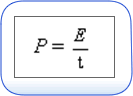
Sabe-se que de dois aquecedores de potências diferentes, ligados durante uma hora, o mais potente aquece uma sala mais rapidamente, isto é, transfere para o meio mais energia por unidade de tempo. A potência relaciona-se com a rapidez com que a energia se transfere.

A potência elétrica, cujo símbolo é P, pode ser definida como a quantidade de energia elétrica transferida por unidade de tempo:

Onde E designa a energia e t o tempo.
    A unidade de potência é o watt (símbolo W), em homenagem ao físico britânico James Watt, que viveu no século XIX. Usa-se com muita freqüência múltiplos do watt como o quilowatt (símbolo KW, igual a mil watts), o megawat (símbolo MW, igual a um milhão de watts) e o gigawatt (símbolo GW, igual a mil milhões de watts):

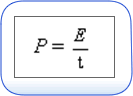
Observando uma conta de luz verifica-se que a energia elétrica é medida em kW h (kilowatt hora).

Um aquecedor com a potência de 1000 W (1 kW), ligado durante uma hora, transfere a energia de um kilowatt hora (1 kWh). A expressão P = E / t pode ser escrita na forma E = P . t, o que mostra como se pode exprimir energia (o kilowatt hora) como o produto de uma unidade de potência (o kilowatt) por uma unidade de tempo (a hora). Pode-se então escrever:
1 kW h = 1 kW . 1 h
    
- Verificando a situação:  

Os aparelhos elétricos domésticos e industriais têm variadas potências (e, conseqüentemente, têm variados "gastos" de energia - e de dinheiro - por hora), conforme se vê na Figura 1.

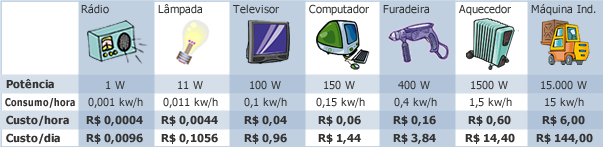
Consideremos dois aparelhos elétricos sujeitos à mesma diferença de potencial. O aparelho mais potente precisa de mais energia por unidade de tempo para funcionar e, por isso, deve ser percorrido por uma corrente elétrica de maior intensidade. Pode-se escrever:
P = V . I
    

Um aparelho com potência de 1 watt, sujeito a uma diferença de potencial de 1 volt é percorrido por uma intensidade de corrente de 1 ampère, isto é:
1 W = 1 V . 1 A
    

A definição de resistência, como foi dito, permite escrever V = R . I (esta é a lei de Ohm se R for constante). Substituindo V por R x I na expressão P = V . I, vem:
P = V . I = R . I . I
isto é,
P=R.I²

    Esta expressão indica que a potência dissipada por efeito Joule num aparelho elétrico é o produto do valor da sua resistência pelo quadrado do valor da intensidade de corrente que o percorre. Tem-se: